Mathieu group
| Group theory |
|---|
| Group theory |
|
Cyclic group Zn
Symmetric group, Sn Dihedral group, Dn Alternating group An Mathieu groups M11, M12, M22, M23, M24 Conway groups Co1, Co2, Co3 Janko groups J1, J2, J3, J4 Fischer groups F22, F23, F24 Baby Monster group B Monster group M |
|
|
|
Solenoid (mathematics)
Circle group General linear group GL(n) Special linear group SL(n) Orthogonal group O(n) Special orthogonal group SO(n) Unitary group U(n) Special unitary group SU(n) Symplectic group Sp(n) Lorentz group Poincaré group Conformal group Diffeomorphism group Loop group Infinite-dimensional Lie groups O(∞) SU(∞) Sp(∞) |
In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered. They are usually denoted by the symbols M11, M12, M22, M23, M24, and can be thought of respectively as permutation groups on sets of 11, 12, 22, 23 or 24 objects (or points).
Sometimes the notation M7, M8, M9, M10, M19, M20 and M21 is used for related groups (which act on sets of 7, 8, 9, 10, 19, 20, and 21 points, respectively), namely the stabilizers of points in the larger groups. While these are not sporadic simple groups, they are important subgroups of the larger groups and can be used to construct the larger ones.[note 1] Conversely, John Conway has suggested that one can extend this sequence up by generalizing the fifteen puzzle, obtaining a subset of the symmetric group on 13 points denoted M13.[1][2]
M24, the largest of the groups, and which contains all the others, is contained within the symmetry group of the binary Golay code, which has practical uses. Moreover, the Mathieu groups are fascinating to many group theorists as mathematical anomalies.
Contents |
History
Simple groups are defined as having no nontrivial proper normal subgroups. Intuitively this means they cannot be broken down in terms of smaller groups. For many years group theorists struggled to classify the simple groups and had found all of them by about 1980. Simple groups belong to a number of infinite families except for 26 groups including the Mathieu groups, called sporadic simple groups. After the Mathieu groups no new sporadic groups were found until 1965, when the group J1 was discovered.
Multiply transitive groups
Mathieu was interested in finding multiply transitive permutation groups, which will now be defined. For a natural number k, a permutation group G acting on n points is k-transitive if, given two sets of points a1, ... ak and b1, ... bk with the property that all the ai are distinct and all the bi are distinct, there is a group element g in G which maps ai to bi for each i between 1 and k. Such a group is called sharply k-transitive if the element g is unique (i.e. the action on k-tuples is regular, rather than just transitive).
M24 is 5-transitive, and M12 is sharply 5-transitive, with the other Mathieu groups (simple or not) being the subgroups corresponding to stabilizers of m points, and accordingly of lower transitivity (M23 is 4-transitive, etc.).
The only 4-transitive groups are the symmetric groups Sk for k at least 4, the alternating groups Ak for k at least 6, and the Mathieu groups M24, M23, M12 and M11. The full proof requires the classification of finite simple groups, but some special cases have been known for much longer.
It is a classical result of Jordan that the symmetric and alternating groups (of degree k and k + 2 respectively), and M12 and M11 are the only sharply k-transitive permutation groups for k at least 4.
Important examples of multiply transitive groups are the 2-transitive groups and the Zassenhaus groups. The Zassenhaus groups notably include the projective general linear group of a projective line over a finite field, PGL(2,Fq), which is sharply 3-transitive (see cross ratio) on 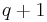 elements.
elements.
Order and transitivity table
| Group | Order | Order (product) | Factorised order | Transitivity | Simple |
|---|---|---|---|---|---|
| M24 | 244823040 | 3·16·20·21·22·23·24 | 210·33·5·7·11·23 | 5-transitive | simple |
| M23 | 10200960 | 3·16·20·21·22·23 | 27·32·5·7·11·23 | 4-transitive | simple |
| M22 | 443520 | 3·16·20·21·22 | 27·32·5·7·11 | 3-transitive | simple |
| M21 | 20160 | 3·16·20·21 | 26·32·5·7 | 2-transitive | simple |
| M20 | 960 | 3·16·20 | 26·3·5 | 1-transitive | not simple |
| M19 | 48 | 3·16 | 24·3 | 0-transitive[note 2] | not simple |
| M12 | 95040 | 8·9·10·11·12 | 26·33·5·11 | sharply 5-transitive | simple |
| M11 | 7920 | 8·9·10·11 | 24·32·5·11 | sharply 4-transitive | simple |
| M10 | 720 | 8·9·10 | 24·32·5 | sharply 3-transitive | not simple |
| M9 | 72 | 8·9 | 23·32 | sharply 2-transitive | not simple |
| M8 | 8 | 8 | 23 | sharply 1-transitive | not simple |
| M7 | 1 | 1 | 1 | sharply 0-transitive | not simple |
Constructions of the Mathieu groups
The Mathieu groups can be constructed in various ways.
Permutation groups
M12 has a simple subgroup of order 660, a maximal subgroup. That subgroup can be represented as a linear fractional group on the field F11 of 11 elements. With -1 written as a and infinity as b , two standard generators are (0123456789a) and (0b)(1a)(25)(37)(48)(69). A third generator giving M12 sends an element x of F11 to 4x2-3x7; as a permutation that is (26a7)(3945). The stabilizer of 4 points is a quaternion group.
Likewise M24 has a maximal simple subgroup of order 6072 and this can be represented as a linear fractional group on the field F23. One generator adds 1 to each element (leaving the point N at infinity fixed), i. e. (0123456789ABCDEFGHIJKLM)(N), and the other is the order reversing permutation, (0N)(1M)(2B)(3F)(4H)(59)(6J)(7D)(8K)(AG)(CL)(EI). A third generator giving M24 sends an element x of F23 to 4x4-3x15; computation shows that as a permutation this is (2G968)(3CDI4)(7HABM)(EJLKF).
These constructions were cited by Carmichael;[3] Dixon and Mortimer ascribe the permutations to Mathieu.[4]
Automorphism groups of Steiner systems
There exists up to equivalence a unique S(5,8,24) Steiner system W24 (the Witt design). The group M24 is the automorphism group of this Steiner system; that is, the set of permutations which map every block to some other block. The subgroups M23 and M22 are defined to be the stabilizers of a single point and two points respectively.
Similarly, there exists up to equivalence a unique S(5,6,12) Steiner system W12, and the group M12 is its automorphism group. The subgroup M11 is the stabilizer of a point.
M24 from PSL(3,4)
M24 can be built starting from PSL(3,4); this is one of the remarkable phenomena of mathematics.
A good nest egg for M24 is PSL(3,4), the projective special linear group of 3-dimensional space over the finite field with 4 elements,[5] also called M21 which acts on the projective plane over the field F4, an S(2,5,21) system called W21. Its 21 blocks are called lines. Any 2 lines intersect at one point.
M21 has 168 simple subgroups of order 360 and 360 simple subgroups of order 168. In the larger projective general linear group PGL(3,4) both sets of subgroups form single conjugacy classes, but in M21 both sets split into 3 conjugacy classes. The subgroups respectively have orbits of 6, called hyperovals, and orbits of 7, called Fano subplanes. These sets allow creation of new blocks for larger Steiner systems. M21 is normal in PGL(3,4), of index 3. PGL(3,4) has an outer automorphism induced by transposing conjugate elements in F4 (the field automorphism). PGL(3,4) can therefore be extended to the group PΓL(3,4) of projective semilinear transformations, which is a split extension of M21 by the symmetric group S3. PΓL(3,4) turns out to have an embedding as a maximal subgroup of M24.[6]
A hyperoval has no 3 points that are colinear. A Fano subplane likewise satisfies suitable uniqueness conditions .
To W21 append 3 new points and let the automorphisms in PΓL(3,4) but not in M21 permute these new points. An S(3,6,22) system W22 is formed by appending just one new point to each of the 21 lines and new blocks are 56 hyperovals conjugate under M21.
An S(5,8,24) system would have 759 blocks, or octads. Append all 3 new points to each line of W21, a different new point to the Fano subplanes in each of the sets of 120, and append appropriate pairs of new points to all the hyperovals. That accounts for all but 210 of the octads. Those remaining octads are subsets of W21 and are symmetric differences of pairs of lines. There are many possible ways to expand the group PΓL(3,4) to M24.
W12
W12 can be constructed from the affine geometry on the vector space F3xF3, an S(2,3,9) system.
An alternative construction of W12 is the 'Kitten' of R.T. Curtis.[7]
Computer programs
There have been notable computer programs written to generate Steiner systems. An introduction to a construction of W24 via the Miracle Octad Generator of R. T. Curtis and Conway's analog for W12, the miniMOG, can be found in the book by Conway and Sloane.
Automorphism group of the Golay code
The group M24 also is the permutation automorphism group of the binary Golay code W, i.e., the group of permutations of coordinates mapping W to itself. Codewords correspond in a natural way to subsets of a set of 24 objects. Those subsets corresponding to codewords with 8 or 12 coordinates equal to 1 are called octads or dodecads respectively. The octads are the blocks of an S(5,8,24) Steiner system and the binary Golay code is the vector space over field F2 spanned by the octads of the Steiner system. The full automorphism group of the binary Golay code has order 212×|M24|, since there are |M24| permutations and 212 sign changes. These can be visualised by permuting and reflecting the coordinates on the vertices of a 24-dimensional cube.
The simple subgroups M23, M22, M12, and M11 can be defined as subgroups of M24, stabilizers respectively of a single coordinate, an ordered pair of coordinates, a dodecad, and a dodecad together with a single coordinate.
M12 has index 2 in its automorphism group. As a subgroup of M24, M12 acts on the second dodecad as an outer automorphic image of its action on the first dodecad. M11 is a subgroup of M23 but not of M22. This representation of M11 has orbits of 11 and 12. The automorphism group of M12 is a maximal subgroup of M24 of index 1288.
There is a very natural connection between the Mathieu groups and the larger Conway groups, because the binary Golay code and the Leech lattice both lie in spaces of dimension 24. The Conway groups in turn are found in the Monster group. Robert Griess refers to the 20 sporadic groups found in the Monster as the Happy Family, and to the Mathieu groups as the first generation.
Dessins d'enfants
The Mathieu groups can be constructed via dessins d'enfants, with the dessin associated to M12 suggestively called "Monsieur Mathieu".[8]
Polyhedral symmetries
M24 can be constructed starting from the symmetries of the Klein quartic (the symmetries of a tessellation of the genus three surface), which is PSL(2,7), which can be augmented by an additional permutation. This permutation can be described by starting with the tiling of the Klein quartic by 20 triangles (with 24 vertices – the 24 points on which the group acts), then forming squares of out some of the 2 triangles, and octagons out of 6 triangles, with the added permutation being "interchange the two endpoints of the lines bisecting the squares and octagons". This can be visualized by coloring the triangles – the corresponding tiling is topologically but not geometrically the t0,1{4, 3, 3} tiling, and can be (polyhedrally) immersed in Euclidean 3-space as the small cubicuboctahedron (which also has 24 vertices).[9]
Properties
The Mathieu groups have fascinating properties; these groups happen because of a confluence of several anomalies of group theory.
For example, M12 contains a copy of the exceptional outer automorphism of S6. M12 contains a subgroup isomorphic to S6 acting differently on 2 sets of 6. In turn M12 has an outer automorphism of index 2 and, as a subgroup of M24, acts differently on 2 sets of 12.
Note also that M10 is a non-split extension of the form A6.2 (an extension of the group of order 2 by A6), and accordingly A6 may be denoted M10′ as it is an index 2 subgroup of M10.
The linear group GL(4,2) has an exceptional isomorphism to the alternating group A8; this isomorphism is important to the structure of M24. The pointwise stabilizer O of an octad is an abelian group of order 16, exponent 2, each of whose involutions moves all 16 points outside the octad. The stabilizer of the octad is a split extension of O by A8.[10] There are 759 (= 3·11·23) octads. Hence the order of M24 is 759*16*20160.
Matrix representations in GL(11,2)
The binary Golay code is a vector space of dimension 12 over F2. The fixed points under M24 form a subspace of 2 vectors, those with coordinates all 0 or all 1. The quotient space, of dimension 11, order 211, can be constructed as a set of partitions of 24 bits into pairs of Golay codewords. It is intriguing that the number of non-zero vectors, 211-1 = 2047, is the smallest Mersenne number with prime exponent that is not prime, equal to 23*89. Then |M24| divides |GL(11,2)| = 255*36*52*73*11*17*23*73*89.
M23 also requires dimension 11.
The groups M22, M12, and M11 are represented in GL(10,2).
Sextet subgroup of M24
Consider a tetrad, any set of 4 points in the Steiner system W24. An octad is determined by choice of a fifth point from the remaining 20. There are 5 octads possible. Hence any tetrad determines a partition into 6 tetrads, called a sextet, whose stabilizer in M24 is called a sextet group.
The total number of tetrads is 24*23*22*21/4! = 23*22*21. Dividing that by 6 gives the number of sextets, 23*11*7 = 1771. Furthermore, a sextet group is a subgroup of a wreath product of order 6!*(4!)6, whose only prime divisors are 2, 3, and 5. Now we know the prime divisors of |M24|. Further analysis would determine the order of the sextet group and hence |M24|.
It is convenient to arrange the 24 points into a 6-by-4 array:
A E I M Q U
B F J N R V
C G K O S W
D H L P T X
Moreover, it is convenient to use the elements of the field F4 to number the rows: 0, 1, u, u2.
The sextet group has a normal abelian subgroup H of order 64, isomorphic to the hexacode, a vector space of length 6 and dimension 3 over F4. A non-zero element in H does double transpositions within 4 or 6 of the columns. Its action can be thought of as addition of vector co-ordinates to row numbers.
The sextet group is a split extension of H by a group 3.S6 (a stem extension). Here is an instance within the Mathieu groups where a simple group (A6) is a subquotient, not a subgroup. 3.S6 is the normalizer in M24 of the subgroup generated by r=(BCD)(FGH)(JKL)(NOP)(RST)(VWX), which can be thought of as a multiplication of row numbers by u2. The subgroup 3.A6 is the centralizer of <r>. Generators of 3.A6 are:
- (AEI)(BFJ)(CGK)(DHL)(RTS)(VWX) (rotating first 3 columns)
- (AQ)(BS)(CT)(DR)(EU)(FX)(GV)(HW)
- (AUEIQ)(BXGKT)(CVHLR)(DWFJS) (product of preceding two)
- (FGH)(JLK)(MQU)(NRV)(OSW)(PTX) (rotating last 3 columns)
An odd permutation of columns, say (CD)(GH)(KL)(OP)(QU)(RV)(SX)(TW), then generates 3.S6.
The group 3.A6 is isomorphic to a subgroup of SL(3,4) whose image in PSL(3,4) has been noted above as the hyperoval group.
The applet Moggie has a function that displays sextets in color.
Subgroup structure
M24 contains non-abelian simple subgroups of 13 isomorphism types: five classes of A5, four classes of PSL(3,2), two classes of A6, two classes of PSL(2,11), one class each of A7, PSL(2,23), M11, PSL(3,4), A8, M12, M22, M23, and M24. A6 has also been noted as a subquotient in the sextet subgroup.
Maximal subgroups of M24
Robert T. Curtis completed the search for maximal subgroups of M24 in (Curtis 1977), which had previously been mistakenly claimed in (Choi 1972b).[11]
The list is as follows:[6]
- M23, order 10200960
- M22:2, order 887040, orbits of 2 and 22
- 24:A8, order 322560, orbits of 8 and 16: octad group
- M12:2, order 190080, transitive and imprimitive: dodecad group
- Copy of M12 acting differently on 2 sets of 12, reflecting outer automorphism of M12
- 26:(3.S6), order 138240: sextet group (vide supra)
- PSL(3,4):S3, order 120960, orbits of 3 and 21
- 26:(PSL(2,7) x S3), order 64512, transitive and imprimitive: trio group.
- Stabilizer of partition into 3 octads.
- The subgroups of type PSL(2,7) have 3 orbits of 8. There also are isomorphic subgroups with orbits of 8, 7, and 7.
- PSL(2,23), order 6072: doubly transitive
- Octern group, order 168, simple, transitive and imprimitive, 8 blocks of 3
- Last maximal subgroup of M24 to be found.
- This group's 7-elements fall into 2 conjugacy classes of 24.
Maximal subgroups of M23
- M22, order 443520
- PSL(3,4):2, order 40320, orbits of 21 and 2
- 24:A7, order 40320, orbits of 7 and 16
- Stabilizer of W23 block
- A8, order 20160, orbits of 8 and 15
- M11, order 7920, orbits of 11 and 12
- (24:A5):S3 or M20:S3, order 5760, orbits of 3 and 20 (5 blocks of 4)
- One-point stabilizer of the sextet group
- 23:11, order 253, simply transitive
Maximal subgroups of M22
There are no proper subgroups transitive on all 22 points.
- PSL(3,4) or M21, order 20160: one-point stabilizer
- 24:A6, order 5760, orbits of 6 and 16
- Stabilizer of W22 block
- A7, order 2520, orbits of 7 and 15
- There are 2 sets, of 15 each, of simple subgroups of order 168. Those of one type have orbits of 7 and 14; the others have orbits of 7, 8, and 7.
- A7, orbits of 7 and 15
- Conjugate to preceding type in M22:2.
- 24:S5, order 1920, orbits of 2 and 20 (5 blocks of 4)
- A 2-point stabilizer in the sextet group
- 23:PSL(3,2), order 1344, orbits of 8 and 14
- M10, order 720, orbits of 10 and 12 (2 blocks of 6)
- A one-point stabilizer of M11 (point in orbit of 11)
- A non-split extension of form A6.2
- PSL(2,11), order 660, orbits of 11 and 11
- Another one-point stabilizer of M11 (point in orbit of 12)
Maximal subgroups of M21
There are no proper subgroups transitive on all 21 points.
- 24:A5 or M20, order 960: one-point stabilizer
- Imprimitive on 5 blocks of 4
- 24:A5, transpose of M20, orbits of 5 and 16
- A6, order 360, orbits of 6 and 15: hyperoval group
- A6, orbits of 6 and 15
- A6, orbits of 6 and 15
- PSL(3,2), order 168, orbits of 7 and 14: Fano subplane group
- PSL(3,2), orbits of 7 and 14
- PSL(3,2), orbits of 7 and 14
- 32:Q or M9, order 72, orbits of 9 and 12
Maximal subgroups of M12
There are 11 conjugacy classes of maximal subgroups, 6 occurring in automorphic pairs.
- M11, order 7920, degree 11
- M11, degree 12
- Outer automorphic image of preceding type
- S6:2, order 1440, imprimitive and transitive, 2 blocks of 6
- Example of the exceptional outer automorphism of S6
- M10.2, order 1440, orbits of 2 and 10
- Outer automorphic image of preceding type
- PSL(2,11), order 660, doubly transitive on the 12 points
- 32:(2.S4), order 432, orbits of 3 and 9
- Isomorphic to the affine group on the space C3 x C3.
- 32:(2.S4), imprimitive on 4 sets of 3
- Outer automorphic image of preceding type
- S5 x 2, order 240, doubly imprimitive, 6 by 2
- Centralizer of a sextuple transposition
- Q:S4, order 192, orbits of 4 and 8.
- Centralizer of a quadruple transposition
- 42:(2 x S3), order 192, imprimitive on 3 sets of 4
- A4 x S3, order 72, doubly imprimitive, 4 by 3
Maximal subgroups of M11
There are 5 conjugacy classes of maximal subgroups.
- M10, order 720, one-point stabilizer in representation of degree 11
- PSL(2,11), order 660, one-point stabilizer in representation of degree 12
- M9:2, order 144, stabilizer of a 9 and 2 partition.
- S5, order 120, orbits of 5 and 6
- Stabilizer of block in the S(4,5,11) Steiner system
- Q:S3, order 48, orbits of 8 and 3
- Centralizer of a quadruple transposition
- Isomorphic to GL(2,3).
Number of elements of each order
The maximum order of any element in M11 is 11. The conjugacy class orders and sizes are found in the ATLAS.[12]
| Order | No. elements | Conjugacy |
|---|---|---|
| 1 = 1 | 1 = 1 | 1 class |
| 2 = 2 | 165 = 3 · 5 · 11 | 1 class |
| 3 = 3 | 440 = 23 · 5 · 11 | 1 class |
| 4 = 22 | 990 = 2 · 32 · 5 · 11 | 1 class |
| 5 = 5 | 1584 = 24 · 32 · 11 | 1 class |
| 6 = 2 · 3 | 1320 = 23 · 3 · 5 · 11 | 1 class |
| 8 = 23 | 1980 = 22 · 32 · 5 · 11 | 2 classes (power equivalent) |
| 11 = 11 | 1440 = 25 · 32 · 5 | 2 classes (power equivalent) |
The maximum order of any element in M12 is 11. The conjugacy class orders and sizes are found in the ATLAS [1].
| Order | No. elements | Conjugacy |
|---|---|---|
| 1 = 1 | 1 = 1 | 1 class |
| 2 = 2 | 891 = 34 · 11 | 2 classes (not power equivalent) |
| 3 = 3 | 4400 = 24 · 52 · 11 | 2 classes (not power equivalent) |
| 4 = 22 | 5940 = 22 · 33 · 5 · 11 | 2 classes (not power equivalent) |
| 5 = 5 | 9504 = 25 · 33 · 11 | 1 class |
| 6 = 2 · 3 | 23760 = 24 · 33 · 5 · 11 | 2 classes (not power equivalent) |
| 8 = 23 | 23760 = 24 · 33 · 5 · 11 | 2 classes (not power equivalent) |
| 10 = 2 · 5 | 9504 = 25 · 33 · 11 | 1 class |
| 11 = 11 | 17280 = 27 · 33 · 5 | 2 classes (power equivalent) |
The maximum order of any element in M21 is 7.
| Order | No. elements | Cycle structure and conjugacy |
|---|---|---|
| 1 = 1 | 1 | 1 class |
| 2 = 2 | 315 = 32 · 5 · 7 | 28, 1 class |
| 3 = 3 | 2240 = 26 · 5 · 7 | 36, 1 class |
| 4 = 22 | 1260 = 22 · 32 · 5 · 7 | 2244, 1 class |
| 1260 = 22 · 32 · 5 · 7 | 2244, 1 class | |
| 1260 = 22 · 32 · 5 · 7 | 2244, 1 class | |
| 5 = 5 | 8064 = 27 · 32 · 7 | 54, 2 power equivalent classes |
| 7 = 7 | 5760 = 27 · 32 · 5 | 73, 2 power equivalent classes |
The maximum order of any element in M22 is 11.
| Order | No. elements | Cycle structure and conjugacy |
|---|---|---|
| 1 = 1 | 1 | 1 class |
| 2 = 2 | 1155 = 3 · 5 · 7 · 11 | 28, 1 class |
| 3 = 3 | 12320 = 25 · 5 · 7 · 11 | 36, 1 class |
| 4 = 22 | 13860 = 22 · 32 · 5 · 7 · 11 | 2244, 1 class |
| 27720 = 23 · 32 · 5 · 7 · 11 | 2244, 1 class | |
| 5 = 5 | 88704 = 27 · 32 · 7 · 11 | 54, 1 class |
| 6 = 2 · 3 | 36960 = 25 · 3 · 5 · 7 · 11 | 223262, 1 class |
| 7 = 7 | 126720 = 28 · 32 · 5 · 11 | 73, 2 power equivalent classes |
| 8 = 23 | 55440 = 24 · 32 · 5 · 7 · 11 | 2·4·82, 1 class |
| 11 = 11 | 80640 = 28 · 32 · 5 · 7 | 112, 2 power equivalent classes |
The maximum order of any element in M23 is 23.
| Order | No. elements | Cycle structure and conjugacy |
|---|---|---|
| 1 = 1 | 1 | 1 class |
| 2 = 2 | 3795 = 3 · 5 · 11 · 23 | 28, 1 class |
| 3 = 3 | 56672 = 25 · 7 · 11 · 23 | 36, 1 class |
| 4 = 22 | 318780 = 22 · 32 · 5 · 7 · 11 · 23 | 2244, 1 class |
| 5 = 5 | 680064 = 27 · 3 · 7 · 11 · 23 | 54, 1 class |
| 6 = 2 · 3 | 850080 = 25 · 3 · 5 · 7 · 11 · 23 | 223262, 1 class |
| 7 = 7 | 1457280 = 27 · 32 · 5 · 11 · 23 | 73, 2 power equivalent classes |
| 8 = 23 | 1275120 = 24 · 32 · 5 · 7 · 11 · 23 | 2·4·82, 1 class |
| 11 = 11 | 1854720 = 28 · 32 · 5 · 7 · 23 | 112, 2 power equivalentclasses |
| 14 = 2 · 7 | 1457280 = 27 · 32 · 5 · 11 · 23 | 2·7·14, 2 power equivalent classes |
| 15 = 3 · 5 | 1360128 = 28 · 3 · 7 · 11 · 23 | 3·5·15, 2 power equivalent classes |
| 23 = 23 | 887040 = 28 · 32 · 5 · 7 · 11 | 23, 2 power equivalent classes, |
The maximum order of any element in M24 is 23. There are 26 conjugacy classes.
| Order | No. elements | Cycle structure and conjugacy |
|---|---|---|
| 1 = 1 | 1 | 1 class |
| 2 = 2 | 11385 = 32 · 5 · 11 · 23 | 28, 1 class |
| 31878 = 2 · 32 · 7 · 11 · 23 | 212, 1 class | |
| 3 = 3 | 226688 = 27 · 7 · 11 · 23 | 36, 1 class |
| 485760 = 27 · 3 · 5 · 11 · 23 | 38, 1 class | |
| 4 = 22 | 637560 = 23 · 32 · 5 · 7 · 11 · 23 | 2444, 1 class |
| 1912680 = 23 · 33 · 5 · 7 · 11 · 23 | 2244, 1 class | |
| 2550240 = 25 · 32 · 5 · 7 · 11 · 23 | 46, 1 class | |
| 5 = 5 | 4080384 = 28 · 33 · 7 · 11 · 23 | 54, 1 class |
| 6 = 2 · 3 | 10200960 = 27 · 32 · 5 · 7 · 11 · 23 | 223262, 1 class |
| 10200960 = 27 · 32 · 5 · 7 · 11 · 23 | 64, 1 class | |
| 7 = 7 | 11658240 = 210 · 32 · 5 · 11 · 23 | 73, 2 power equivalent classes |
| 8 = 23 | 15301440 = 26 · 33 · 5 · 7 · 11 · 23 | 2·4·82, 1 class |
| 10 = 2 · 5 | 12241152 = 28 · 33 · 7 · 11 · 23 | 22102, 1 class |
| 11 = 11 | 22256640 = 210 · 33 · 5 · 7 · 23 | 112, 1 class |
| 12 = 22 · 3 | 20401920 = 28 · 32 · 5 · 7 · 11 · 23 | 2 ·4·6·12, 1 class |
| 20401920 = 28 · 32 · 5 · 7 · 11 · 23 | 122, 1 class | |
| 14 = 2 · 7 | 34974720 = 210 · 33 · 5 · 11 · 23 | 2·7·14, 2 power equivalent classes |
| 15 = 3 · 5 | 32643072 = 211 · 32 · 7 · 11 · 23 | 3·5·15, 2 power equivalent classes |
| 21 = 3 · 7 | 23316480 = 211 · 32 · 5 · 11 · 23 | 3·21, 2 power equivalent classes |
| 23 = 23 | 21288960 = 211 · 33 · 5 · 7 · 11 | 23, 2 power equivalent classes |
Notes
- ^ M7 is the trivial group, while M19 does not act transitively on 19 points and 19 does not divide its order, so this sequence cannot be extended further down.
- ^ M19 acts non-trivially but intransitively on 19 points, and has order 3·16; note that
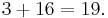 In fact, it has 2 orbits: one of order 16, one of order 3 (the Sylow 2-subgroup acts regularly on 16 points, fixing the other 3, while the Sylow 3-subgroup permutes the 3 points, fixing the order 16 orbit). See (Choi 1972a, p. 4) for details.
In fact, it has 2 orbits: one of order 16, one of order 3 (the Sylow 2-subgroup acts regularly on 16 points, fixing the other 3, while the Sylow 3-subgroup permutes the 3 points, fixing the order 16 orbit). See (Choi 1972a, p. 4) for details.
References
- ^ John H. Conway, "Graphs and Groups and M13", Notes from New York Graph Theory Day XIV (1987), pp. 18–29.
- ^ Conway, John Horton; Elkies, Noam D.; Martin, Jeremy L. (2006), "The Mathieu group M12 and its pseudogroup extension M13", Experimental Mathematics 15 (2): 223–236, ISSN 1058-6458, MR2253008, http://nrs.harvard.edu/urn-3:HUL.InstRepos:2794826
- ^ Carmichael (1937): pp.151, 164, 263.
- ^ Dixon and Mortimer (1996): p. 209.
- ^ (Dixon & Mortimer 1996, pp. 192–205)
- ^ a b (Griess 1998, p. 55)
- ^ (Curtis 1984)
- ^ le Bruyn, Lieven (1 March 2007), Monsieur Mathieu, http://www.neverendingbooks.org/index.php/monsieur-mathieu.html.
- ^ (Richter)
- ^ Thomas Thompson (1983), pp. 197-208.
- ^ (Griess 1998, p. 54)
- ^ ATLAS: Mathieu group M11
- Mathieu E., Mémoire sur l'étude des fonctions de plusieurs quantités, sur la manière de les former et sur les substitutions qui les laissent invariables J. Math. Pures Appl. (Liouville) (2) VI, 1861, pp. 241–323.
- Mathieu E., Sur la fonction cinq fois transitive de 24 quantités, Liouville Journ., (2) XVIII., 1873, pp. 25–47.
- Carmichael, Robert D. Groups of Finite Order, Dover (1937, reprint 1956).
- Conway, J.H.; Sloane N.J.A. Sphere Packings, Lattices and Groups: v. 290 (Grundlehren Der Mathematischen Wissenschaften.) Springer Verlag. ISBN 0-387-98585-9
- Choi, C. (May 1972a), "On Subgroups of M24. I: Stabilizers of Subsets", Transactions of the American Mathematical Society (American Mathematical Society) 167: 1–27, doi:10.2307/1996123, JSTOR 1996123
- Choi, C. (May 1972b). "On Subgroups of M24. II: the Maximal Subgroups of M24". Transactions of the American Mathematical Society (American Mathematical Society) 167: 29–47. doi:10.2307/1996124. JSTOR 1996124.
- Curtis, R. T. A new combinatorial approach to M24. Math. Proc. Camb. Phil. Soc. 79 (1976) 25-42.
- Curtis, R. T. The maximal subgroups of M24. Math. Proc. Camb. Phil. Soc. 81 (1977) 185-192.
- Thompson, Thomas M.: From Error Correcting Codes through Sphere Packings to Simple Groups, Carus Mathematical Monographs, Mathematical Association of America, 1983.
- Curtis, R. T. The Steiner System S(5,6,12), the Mathieu Group M12 and the 'Kitten', Computational Group Theory, Academic Press, London, 1984
- Cuypers, Hans, The Mathieu groups and their geometries, http://www.win.tue.nl/~hansc/mathieu.pdf
- Conway, J. H.; Curtis, R. T.; Norton, S. P.; Parker, R. A.; Wilson, R. A. (1985). Atlas of finite groups. Maximal subgroups and ordinary characters for simple groups. With computational assistance from J. G. Thackray. Eynsham: Oxford University Press. ISBN 0-19-853199-0
- Dixon, John D.; Mortimer, Brian (1996), Permutation Groups, Springer-Verlag
- Griess, Robert L.: Twelve Sporadic Groups, Springer-Verlag, 1998.
- Ronan M. "Symmetry and the Monster", Oxford University Press (2006) ISBN 0-19-280722-6 (an introduction for the lay reader, describing the Mathieu groups in a historical context)
- Richter, David A., How to Make the Mathieu Group M24, http://homepages.wmich.edu/~drichter/mathieu.htm, retrieved 2010-04-15
External links
- Moggie Java applet for studying the Curtis MOG construction
- Scientific American A set of puzzles based on the mathematics of the Mathieu groups
- Sporadic M12 An iPhone app that implements puzzles based on M12, presented as one "spin" permutation and a selectable "swap" permutation
- Octad of the week